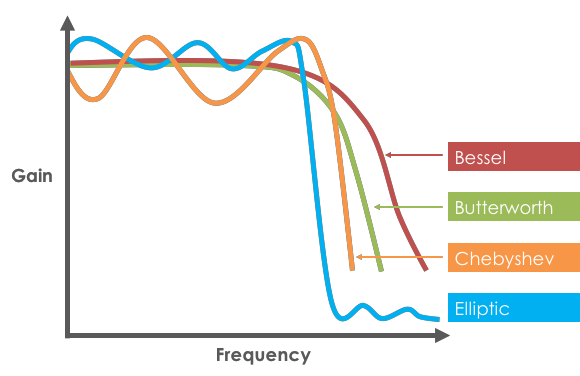
It's time for a good ol'fashion battle royal between the greats of the electronic filter world! In this post, we'll take a closer look at the most popular RF filter typologies: Butterworth, Chebyshev, Bessel, and Elliptic. Each filter types has it's own strengths depending on the application. We'll take a deeper look at each and then do a final comparison between them to see if we can crown a winner in this battle for the ages! Let's get ready to rumble...
Bessel Filter
- Named after: German Mathematician Friedrich Bessel
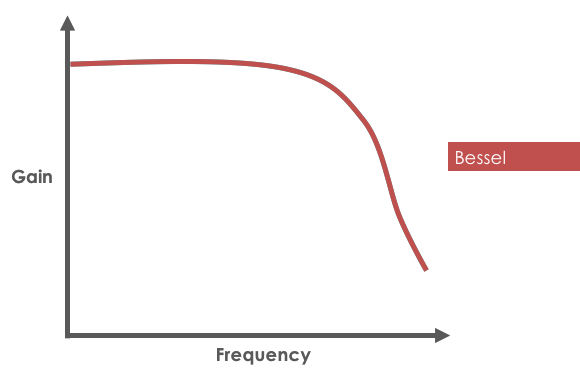
- Bessel filter response:
- Notable features:
The Bessel filter has the gentlest response of the group. Even though it doesn't have a sharp cutoff, it offers superior phase shift (delay) compared to the other filters in the group. The Bessel filter requires the most stages (i.e. most components); however, it offers excellent characteristics: low sensitivity to component tolerance, superior step response.
- Best used for:
The Bessel filter is ideal for applications that require minimal phase shift. Due to the gentle frequency response of the Bessel filter, it can only be used in applications where there is adequate space between the passband and stopband.
Butterworth Filter
- Named after: It’s buttery-smooth response British Physicist Stephen Butterworth
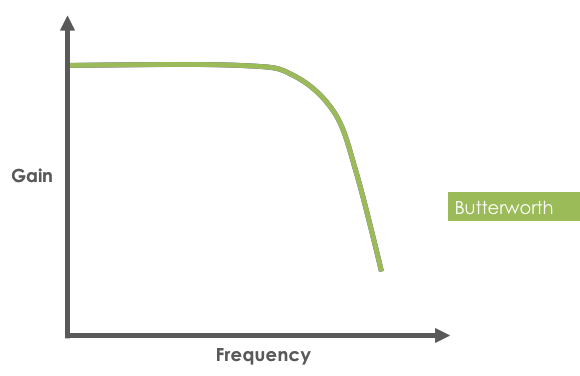
- Butterworth filter response:
- Notable features:
The Butterworth filter is commonly referred to as the "maximally flat" option because the passband response offers the steepest roll-off without inducing a passband ripple. In addition to the flat passband response, the selectivity of the Butterworth filter is better than many other filter typologies such as the Bessel or Gaussian. The flip-side of this improved selectivity is greater delay and poorer phase linearity. Butterworth filters offer solid performance considering the number of components needed to implement the filter.
- Best used for:
Butterworth filters are typically forgiving to part tolerances and values of discrete elements (capacitors, inductors, and resistors). For most bandpass designs, the (Voltage Standing Wave Ratio) VSWR at center frequency is extremely good.
Chebyshev Filter
- Named after: Russian mathematician Pafnuty Chebyshev
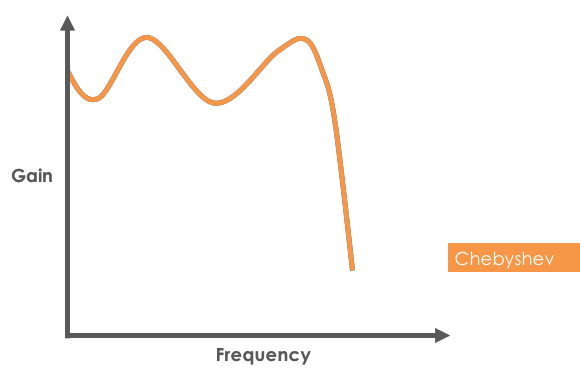
- Chebyshev filter response:
- Notable features:
The Chebyshev filter is known for it's ripple response. This ripple response can be designed to be present in the passband (Chebyshev Type 1) or in the stopband (Chebyshev Type 2). The amplitude of the ripple is directly proportional to steepness of the rolloff. That is, if you want a steeper response, you'll see a larger ripple response. These filters offer performance between that of Elliptic function filters and Butterworth filters. The phase response of the Chebyshev filter is relatively non-linear, which ultimately wreaks havoc on demodulators because it tends to distort pulses because of the non-linear delays. The most common work-around for this phenomena is to increase the bandwidth of the Chebyshev filter to push this non-linear region further out. - Best used for:
The Chebyshev filter is the workhorse of the common filter typologies. It's response is easily realised with few componets and offers very good selectivity with one of the steepest roll-off responses of the group.
Elliptic (Cauer) Filter
- Named after: German Mathematician Wilhelm Cauer
- Elliptic filter response:
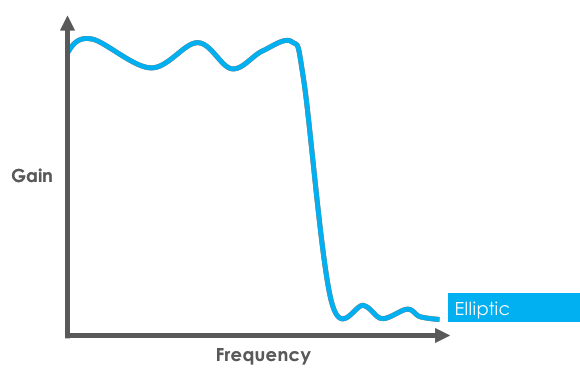
- Notable features:
The elliptic filters is characterized by ripple that exists in both the passband, as well as the stopband. The passband ripple of the elliptic filter is similar to the Chebyshev filter, however the selectivity is greatly improved. The downside to this improved selectivity is a more complex filter network that requires more components. The elliptic filter also has the sharpest roll-off of all filters in this group. This sharp roll-off comes with the unitended consequince of ripples in both the passband and stopband (shown above).
- Best used for:
Despite the passband and stopband ripple, the elliptic filter is best used in applications where selectivity is a key driver in the filter design. The elliptic filter's ripple amplitude of the passband and stopband can be adjusted seperately to fit the application.
... and the winner is?
It depends on the application! That may be an unsatifying answer but it really does depend on many different elements that must be traded during the filter design process such as:
- Frequency response
- Selectivity
- Number of stages (complexity)
- Phase delay
- Ability to pronounce it properly (don't want to look silly in front of your peers ;)
Working on a new filter design for your RF project?
Check out these great resources:
- Filter Wizard from Analog Devices
- 5 Tips to Effective Design Reviews
- RF Design Guide from Bliley Technologies
