
So, What is Phase Coherence?
…More Importantly, Does it Affect You?
First, let’s look at that first question: What is phase coherence?
After little research, it seems that there are several definitions out there. Two definitions that we like are listed below.
- In many ways, the term 'Phase-coherent' is not strictly defined. Often, it is interpreted as signals/systems operating at the same frequency with a consistent phase relationship.
- In physics, two wave sources are perfectly coherent if they have a constant phase difference and the same frequency.
These are both great definitions, although I have a feeling you may be thinking to yourself:
"Ok...Got it! However, I'm still confused. What do these definitions REALLY mean?"
These are two common ways of looking at phase coherence, but what do they really mean? Let’s take a closer look…
A better way to look at the problem might be to split it into two simpler questions.
- How stable is the phase between the two waves (electrical, light, etc.)?
- Does it change quickly with time?
With two perfect sine waves of the same frequency, the relative phase never changes. When the two waves are always shifted by the same amount (Fig. 1), they’re said to be coherent. However, no real wave is perfectly sinusoidal. Also, the two frequencies aren’t always exactly the same. Instead think of a signal that looks sinusoidal in any small piece but the phase is slowly drifting (Fig. 2).
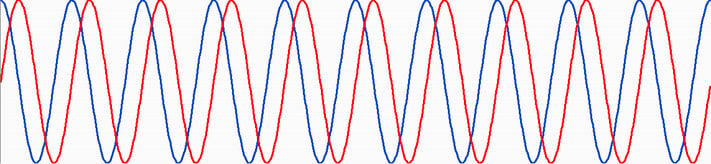
Fig. 1
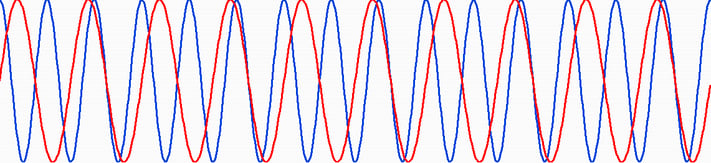
Fig. 2
Fig. 1 is coherent. The relative difference between any two matching points is exactly the same. Fig. 2 is not coherent. The relative difference is always fluctuating.
The figures above represent the ideal and the worst case. As with everything, real life is somewhere in the middle. Something like Fig. 3 below would be more common to see. In the broad spectrum of the graph, the signals aren’t coherent. But if you look at a small time segment (a few cycles), they are close to being coherent.
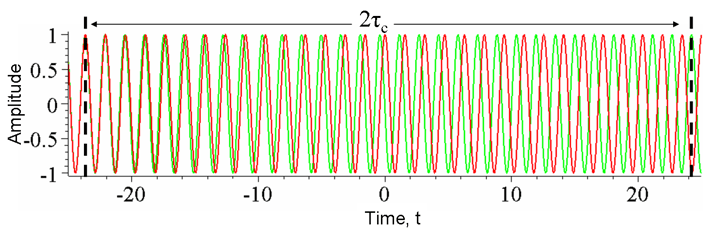
Fig. 3
Looking at it this way, the signals are said to have a “coherence time”. If the phase difference of the two waves is the same, they are coherent. More generally, if the phase difference of two waves remains the same during this "coherence time", they are coherent during that time. In reality, the waves do not remain coherent for an infinite interval and after the coherence time the phase difference drifts.
Now the next question: How does phase coherence affect you?
This phase difference can impact a lot of different fields. Phase is a property of sinusoidal signals (which is pretty much all electronic signals, thanks to Fourier series analysis). So, for example, things like lasers, semiconductor devices, radar, radio receivers, power grids, etc. all can have situations where "electronic phase coherence" is a potential problem. That's already a pretty broad list and there are dozens more.
The biggest worry of this difference is interference, which isn’t always a bad thing. Interference is nothing more than the addition, in the mathematical sense, of wave functions. When interfering, two waves can add together to create a wave of greater amplitude than either one (constructive interference) as in Fig. 4 left or subtract from each other to create a wave of lesser amplitude than either one (destructive interference) as in Fig 4 right, depending on their relative phase.
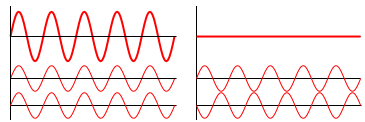
Fig. 4
Either “interference” can be useful depending on the application.
The bottom line: think of signals as waves or vectors. If they are coherent then they add up constructively and if they are non-coherent then they may cancel each other or fading occurs.
How to Avoid Future Phase Coherence Problems
One way many industries avoid coherence problems is by using a Phase-locked loop or PLL. A PLL is a fundamental concept widely used for different purposes in various fields of electrical engineering (e.g. communications, instrumentation, control system, and multimedia). The main idea of phase-locking is the ability to generate a sinusoidal signal whose phase is coherently following that of the main component of the input signal.





